The simplest model of a battery comprises an ideal voltage source that connects in series with a resistance whose value—often a few milliohms—depends on the battery's electrochemical condition and construction. If you attempt to use an ordinary ac milliohmmeter containing a kilohertz-range ac excitation source to measure a battery's internal resistance, you get erroneous results due to capacitive effects, which introduce losses. A more realistic battery model includes a resistive divider that a capacitor partially shunts (Figure 1). In addition, a battery's no-load internal resistances may differ significantly from their values under a full load. Thus, for greatest accuracy, you must measure internal resistance under full load at or near dc.
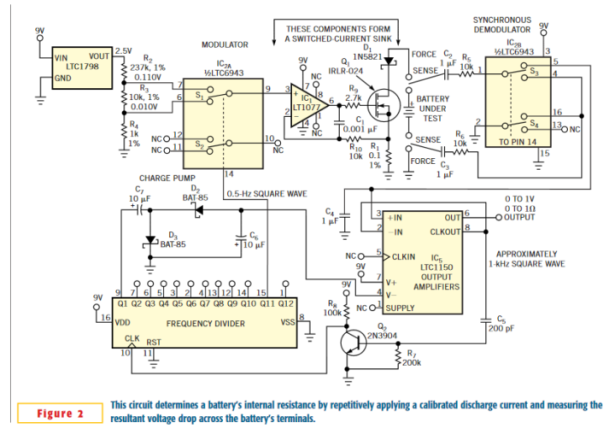
The circuit in Figure 2 meets these requirements and accurately measures internal resistance over a range of 0.001 to 1Ω at battery voltages as high as 13V. One section of an LTC6943 analog switch, IC2A, alternately applies 0.110 and 0.010V derived from 2.5V voltage reference IC3 and resistive divider R2, R3, and R4 to IC1‘s input.
Amplifier IC1, power MOSFET Q1, and associated components form a closed-loop current sink that provides an active load for the battery under test via Q1‘s drain. Diode D1 provides reversed-battery protection. The voltage at amplifier IC1‘s positive input and the voltage drop across R1 determine the load applied to the battery. In operation, the circuit applies a constant-current load comprising a 1A, 0.5-Hz square wave biased at 100 mA to the battery.
The battery's internal resistance develops a 0.5-Hz amplitude-modulated square-wave signal at the Kelvin connections attached to the battery. A synchronous demodulator comprising analog switches S2 and S3 in IC2B and chopper-stabilized amplifier IC5 processes the sensed signal and delivers a 0 to 1V analog output that corresponds to a battery-resistance range of 0 to 1Ω.
For More Details: Dynamic-load circuit determines a battery's internal resistance