N.B. This is new and still being tested.
The provided Python examples showcase different single-channel filters that can be used to manipulate sensor data. The filter functions are only numeric operations and should operate on any Python or CircuitPython system. This enables testing without an internet connection, as they can be fixed and assessed on a regular personal computer.
The code prioritizes clarity over efficiency when being written. Using slab or numpy to apply filters to sample vectors or matrices can often lead to a substantial increase in speed.
The source files can be browsed in raw form in the CircuitPython signals code folder. The files may be also downloaded in a single archive file as signals.zip.
linear.py
An important step in signal processing is applying a calibration transformation to translate raw values received from an analog to a digital converter (ADC) into repeatable and meaningful units. For linear sensors, this can be a two-parameter linear mapping that applies an offset and scaling. One convenient implementation is the map function.map(x, in_min, in_max, out_min, out_max)
Map an input x from range (in_min, in_max) to range (out_min, out_max). This is a Python implementation of the Arduino map() function. Works on either integers or floating point.constrain(x, a, b)
Constrains a number x to be within range (a, b). Python implementation of the Arduino constrains () function. N.B. is included here for convenience, but this is not a linear function.
linear.py: platform-independent linear transforms
No copyright, 2020-2021, Garth Zeglin. This file is explicitly placed in the public domain.
def map(x, in_min, in_max, out_min, out_max):
“””Map an input x from range (in_min, in_max) to range (out_min, out_max). This
is a Python implementation of the Arduino map() function. Works on either
integers or floating point.
“””
divisor = in_max – in_min
if divisor == 0:
return out_min
else:
return ((x - in_min) * (out_max - out_min) / divisor) + out_mindef constrain(x, a, b):
“””Constrains a number x to be within range (a, b). Python implementation
of the Arduino constrain() function.”””
return min(max(x, a), b)
statistics.py
class CentralMeasures
An object that contains multiple accumulators to compute the average, standard deviation, lowest, and highest values from a series of inputs. All attributes are accessible as object properties (i.e. instance variables).
# statistics.py : compute single-channel central measures in an accumulator
# No copyright, 2009-2021, Garth Zeglin. This file is explicitly placed in the public domain.
import math
# CircuitPython lacks math.inf, here is a workaround:
try:
inf_value = math.inf
except AttributeError:
inf_value = math.exp(10000)
class CentralMeasures:
def __init__(self):
"""Object to accumulate central measures statistics on a single channel of data."""
self.samples = 0 # running sum of value^0, i.e., the number of samples
self.total = 0 # running sum of value^1, i.e., the accumulated total
self.squared = 0 # running sum of value^2, i.e., the accumulated sum of squares
self.minval = inf_value # smallest input seen
self.maxval = -inf_value # largest input seen
self.last = 0 # most recent input
# computed statistics
self.average = 0 # mean value
self.variance = 0 # square of the standard deviation
return
def update(self, value):
"""Apply a new sample to the accumulators and update the computed statistics.
Returns the computed average and variance as a tuple."""
self.total += value
self.squared += value * value
if value < self.minval:
self.minval = value
if value > self.maxval:
self.maxval = value
self.samples += 1
self.last = value
# recalculate average and variance
if self.samples > 0:
self.average = self.total / self.samples
if self.samples > 1:
# The "standard deviation of the sample", which is only correct
# if the population is normally distributed and a large sample
# is available, otherwise tends to be too low:
# self.sigma = math.sqrt((self.samples * self.squared - self.total*self.total) /
# self.samples))
# Instead compute the "sample standard deviation", an unbiased
# estimator for the variance. The standard deviation is the
# square root of the variance.
self.variance = ((self.samples * self.squared - self.total*self.total) /
(self.samples * (self.samples - 1)))
return self.average, self.variance
hysteresis.py
Hysteresis is when a system’s behavior is influenced by its past experiences. In physical systems, it shows the existence of a concealed condition, such as the magnetization of a substance. In a filter, non-linear behavior can be beneficial for discretizing data or removing outliers.
class Hysteresis
Filter to quantize an input stream into a binary state. Dual thresholds are needed to implement hysteresis: the input needs to rise above the upper threshold to trigger a high output, then drop below the input threshold to return to the low output. One bit of state is required.class Suppress
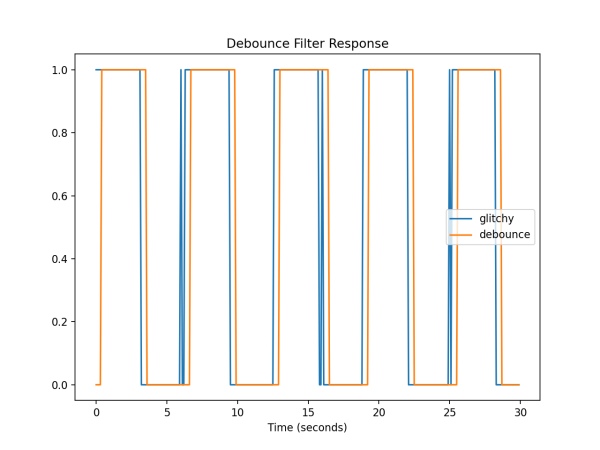
Filter to suppress a specific value in an input stream.class Debounce
Filter to ‘debounce’ an integer stream by suppressing changes from the previous value until a specific new value has been observed a minimum number of times.
# hysteresis.py : platform-independent non-linear filters
# No copyright, 2020-2011, Garth Zeglin. This file is explicitly placed in
# the public domain.
#--------------------------------------------------------------------------------
class Hysteresis:
def __init__(self, lower=16000, upper=48000):
"""Filter to quantize an input stream into a binary state. Dual thresholds are
needed to implement hysteresis: the input needs to rise above the upper
threshold to trigger a high output, then drop below the input threshold
to return to the low output. One bit of state is required.
"""
self.lower = lower
self.upper = upper
self.state = False
def update(self, input):
"""Apply a new sample value to the quantizing filter. Returns a boolean state."""
if self.state is True:
if input < self.lower:
self.state = False
else:
if input > self.upper:
self.state = True
return self.state
#--------------------------------------------------------------------------------
class Suppress:
def __init__(self, value=0):
"""Filter to suppress a specific value in an input stream."""
self.suppress = value
self.previous = None
def update(self, input):
if input != self.suppress:
self.previous = input
return self.previous
#--------------------------------------------------------------------------------
class Debounce:
def __init__(self, samples=5):
"""Filter to 'debounce' an integer stream by suppressing changes from the previous value
until a specific new value has been observed a minimum number of times."""
self.samples = samples # number of samples required to change
self.current_value = 0 # current stable value
self.new_value = None # possible new value
self.count = 0 # count of new values observed
def update(self, input):
if input == self.current_value:
# if the input is unchanged, keep the counter at zero
self.count = 0
self.new_value = None
else:
if input != self.new_value:
# start a new count
self.new_value = input
self.count = 1
else:
# count repeated changes
self.count += 1
if self.count >= self.samples:
# switch state after a sufficient number of changes
self.current_value = self.new_value
self.count = 0
self.new_value = None
return self.current_value
smoothing.py
class Smoothing
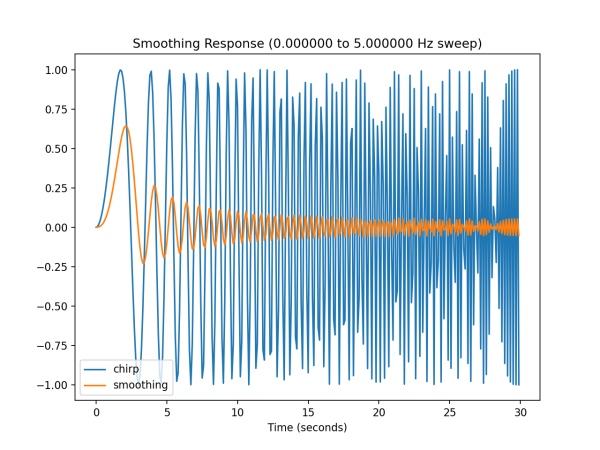
Filter to smooth an input signal using a first-order filter. One state value is required. The smaller the coefficient, the smoother the output.
class MovingAverage
Filter to smooth a signal by averaging over multiple samples. The recent time history (the ‘moving window’) is kept in an array along with a running total. The window size determines how many samples are held in memory and averaged together.
# smoothing.py : platform-independent first-order smoothing filter
# No copyright, 2020-2021, Garth Zeglin. This file is explicitly placed in the public domain.
class Smoothing:
def __init__(self, coeff=0.1):
"""Filter to smooth an input signal using a first-order filter. One state value
is required. The smaller the coefficient, the smoother the output."""
self.coeff = coeff
self.value = 0
def update(self, input):
# compute the error between the input and the accumulator
difference = input - self.value
# apply a constant coefficient to move the smoothed value toward the input
self.value += self.coeff * difference
return self.value
#--------------------------------------------------------------------------------
class MovingAverage:
def __init__(self, window_size=5):
"""Filter to smooth a signal by averaging over multiple samples. The recent
time history (the 'moving window') is kept in an array along with a
running total. The window size determines how many samples are held in
memory and averaged together.
"""
self.window_size = window_size
self.ring = [0] * window_size # ring buffer for recent time history
self.oldest = 0 # index of oldest sample
self.total = 0 # sum of all values in the buffer
def update(self, input):
# subtract the oldest sample from the running total before overwriting
self.total = self.total - self.ring[self.oldest]
# save the new sample by overwriting the oldest sample
self.ring[self.oldest] = input
# advance to the next position, wrapping around as needed
self.oldest += 1
if self.oldest >= self.window_size:
self.oldest = 0
# add the new input value to the running total
self.total = self.total + input
# calculate and return the average
return self.total / self.window_size
median.py
class MedianFilter
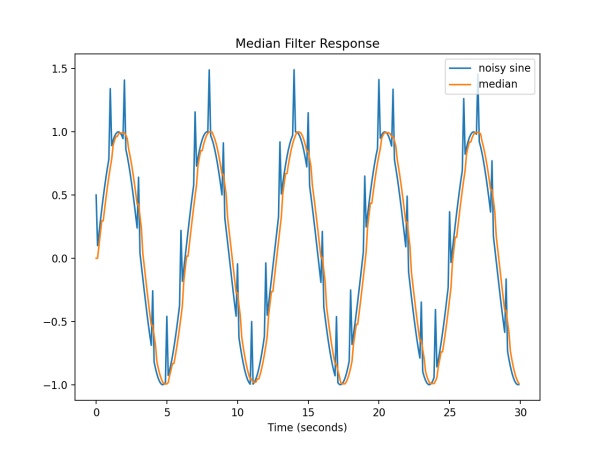
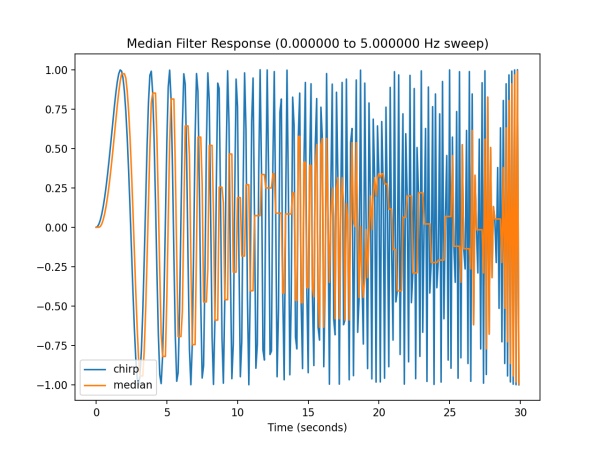
Non-linear filter to reduce signal outliers by returning the median value of the recent history. The window size determines how many samples are held in memory. An input change is typically delayed by half the window width. This filter is useful for throwing away isolated outliers, especially glitches out of range.
# median.py : platform-independent median filter
# No copyright, 2020-2021, Garth Zeglin. This file is explicitly placed in the public domain.
class MedianFilter:
def __init__(self, window_size=5):
"""Non-linear filter to reduce signal outliers by returning the median value
of the recent history. The window size determines how many samples
are held in memory. An input change is typically delayed by half the
window width. This filter is useful for throwing away isolated
outliers, especially glitches out of range.
"""
self.window_size = window_size
self.ring = [0] * window_size # ring buffer for recent time history
self.oldest = 0 # index of oldest sample
def update(self, input):
# save the new sample by overwriting the oldest sample
self.ring[self.oldest] = input
self.oldest += 1
if self.oldest >= self.window_size:
self.oldest = 0
# create a new sorted array from the ring buffer values
in_order = sorted(self.ring)
# return the value in the middle
return in_order[self.window_size//2]
biquad.py
class BiquadFilter
General IIR digital filter using cascaded biquad sections. The specific filter type is configured using a coefficient matrix. These matrices can be generated for low-pass, high-pass, and band-pass configurations.
The file also contains filter matrices automatically generated using filter_gen.py and the SciPy toolkit. In general you will need to regenerate the filter coefficients for your particular application needs. The sample filter responses are shown below.
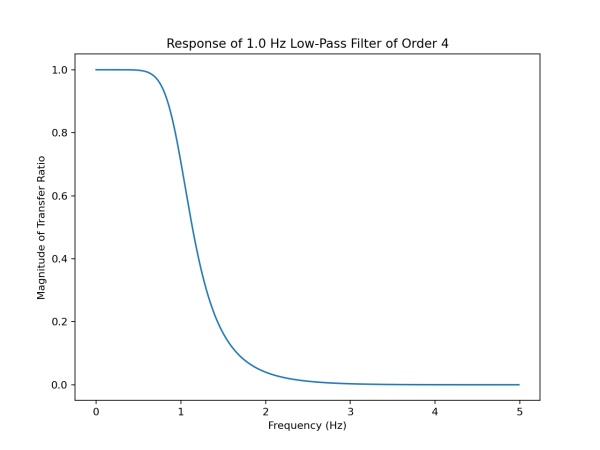
On the left is the low-pass filter signal transfer ratio as a function of frequency. Please note this is plotted on a linear scale for clarity; on a logarithmic scale (dB) the rolloff slope becomes straight. On the right is the low-pass filter time response to a ‘chirp’ frequency sweep.
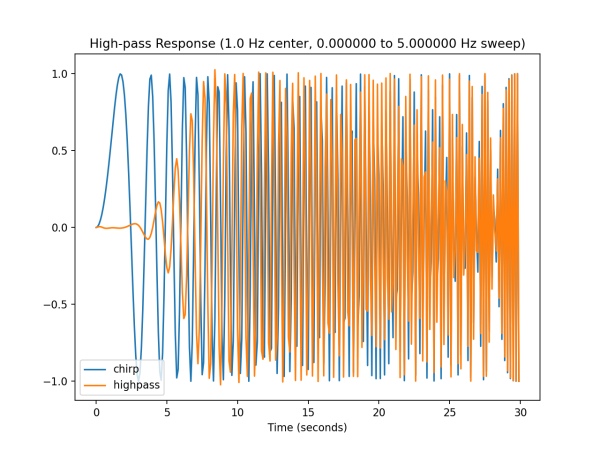
On the left is the high-pass filter signal transfer ratio as a function of frequency, on the right is the time response.
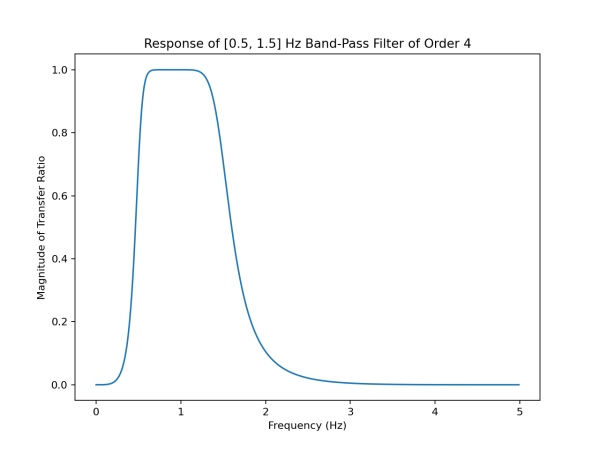
On the left is the band-pass signal transfer ratio as a function of frequency, on the right is the time response.
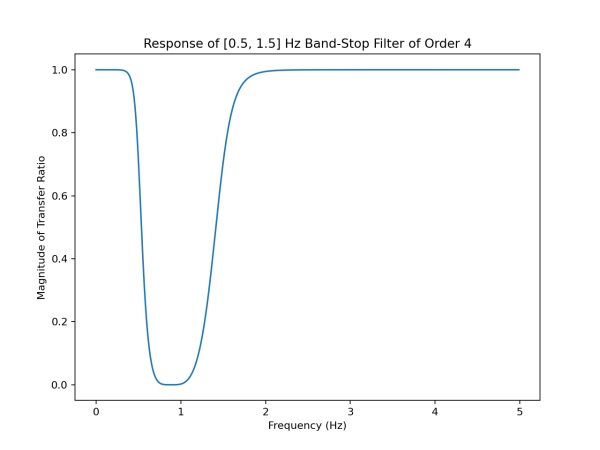
On the left is the band-stop signal transfer ratio as a function of frequency, on the right is the time response.
# biquad.py : digital IIR filters using cascaded biquad sections generated using filter_gen.py.
#--------------------------------------------------------------------------------
# Coefficients for a low-pass Butterworth IIR digital filter with sampling rate
# 10 Hz and corner frequency 1.0 Hz. Filter is order 4, implemented as
# second-order sections (biquads).
# Reference: https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.butter.html
low_pass_10_1 = [[[1.0, -1.04859958, 0.29614036], # A coefficients, first section
[0.00482434, 0.00964869, 0.00482434]], # B coefficients, first section
[[1.0, -1.32091343, 0.63273879], # A coefficients, second section
[1.0, 2.0, 1.0]]] # B coefficients, second section
#--------------------------------------------------------------------------------
# Coefficients for a high-pass Butterworth IIR digital filter with
# sampling rate: 10 Hz and corner frequency 1.0 Hz.
# Filter is order 4, implemented as second-order sections (biquads).
high_pass_10_1 = [[[1.0, -1.04859958, 0.29614036],
[0.43284664, -0.86569329, 0.43284664]],
[[1.0, -1.32091343, 0.63273879],
[1.0, -2.0, 1.0]]]
#--------------------------------------------------------------------------------
# Coefficients for a band-pass Butterworth IIR digital filter with sampling rate
# 10 Hz and pass frequency range [0.5, 1.5] Hz. Filter is order 4, implemented
# as second-order sections (biquads).
band_pass_10_1 = [[[1.0, -1.10547167, 0.46872661],
[0.00482434, 0.00964869, 0.00482434]],
[[1.0, -1.48782202, 0.63179763],
[1.0, 2.0, 1.0]],
[[1.0, -1.04431445, 0.72062964],
[1.0, -2.0, 1.0]],
[[1.0, -1.78062325, 0.87803603],
[1, -2.0, 1.0]]]
#--------------------------------------------------------------------------------
# Coefficients for a band-stop Butterworth IIR digital filter with
# sampling rate: 10 Hz and exclusion frequency range [0.5, 1.5] Hz.
# Filter is order 4, implemented as second-order sections (biquads).
band_stop_10_1 = [[[1.0, -1.10547167, 0.46872661],
[0.43284664, -0.73640270, 0.43284664]],
[[1.0, -1.48782202, 0.63179763],
[1.0, -1.70130162, 1.0]],
[[1.0, -1.04431445, 0.72062964],
[1.0, -1.70130162, 1.0]],
[[1.0, -1.78062325, 0.87803603],
[1.0, -1.70130162, 1.0]]]
#--------------------------------------------------------------------------------
class BiquadFilter:
def __init__(self, coeff=low_pass_10_1):
"""General IIR digital filter using cascaded biquad sections. The specific
filter type is configured using a coefficient matrix. These matrices can be
generated for low-pass, high-pass, and band-pass configurations.
"""
self.coeff = coeff # coefficient matricies
self.sections = len(self.coeff) # number of biquad sections in chain
self.state = [[0,0] for i in range(self.sections)] # biquad state vectors
def update(self, input):
# Iterate over the biquads in sequence. The accum variable transfers
# the input into the chain, the output of each section into the input of
# the next, and final output value.
accum = input
for s in range(self.sections):
A = self.coeff[s][0]
B = self.coeff[s][1]
Z = self.state[s]
x = accum - A[1]*Z[0] - A[2]*Z[1]
accum = B[0]*x + B[1]*Z[0] + B[2]*Z[1]
Z[1] = Z[0]
Z[0] = x
return accum
demo.py
This following script applies all the sample filters to an analog sample stream. This file should be copied into the top-level folder as code.py, and the individual filter samples under their own names so they may be loaded as modules.
# demo.py
# Raspberry Pi Pico - Signal Processing Demo
# Read an analog input with the ADC, apply various filters, and print filtered
# data to the console for plotting.
# Import CircuitPython modules.
import board
import time
import analogio
import digitalio
# Import every filter sample. These files should be copied to the top-level
# directory of the CIRCUITPY filesystem on the Pico.
import biquad
import hysteresis
import linear
import median
import smoothing
import statistics
#---------------------------------------------------------------
# Set up the hardware.
# Set up an analog input on ADC0 (GP26), which is physically pin 31.
# E.g., this may be attached to photocell or photointerrupter with associated pullup resistor.
sensor = analogio.AnalogIn(board.A0)
#---------------------------------------------------------------
# Initialize filter objects as global variables.
stats = statistics.CentralMeasures()
hysteresis = hysteresis.Hysteresis(lower=0.25, upper=0.75)
average = smoothing.MovingAverage()
smoothing = smoothing.Smoothing()
median = median.MedianFilter()
lowpass = biquad.BiquadFilter(biquad.low_pass_10_1)
highpass = biquad.BiquadFilter(biquad.high_pass_10_1)
bandpass = biquad.BiquadFilter(biquad.band_pass_10_1)
bandstop = biquad.BiquadFilter(biquad.band_stop_10_1)
# Collect all the filters in a list for efficient multiple updates.
all_filters = [ stats, hysteresis, average, smoothing, median,
lowpass, highpass, bandpass, bandstop, ]
#---------------------------------------------------------------
# Run the main event loop.
# Use the high-precision clock to regulate a precise *average* sampling rate.
sampling_interval = 100000000 # 0.1 sec period of 10 Hz in nanoseconds
next_sample_time = time.monotonic_ns()
while True:
# read the current nanosecond clock
now = time.monotonic_ns()
if now >= next_sample_time:
# Advance the next event time; by spacing out the timestamps at precise
# intervals, the individual sample times may have 'jitter', but the
# average rate will be exact.
next_sample_time += sampling_interval
# Read the sensor once per sampling cycle.
raw = sensor.value
# Apply calibration to map integer ADC values to meaningful units. The
# exact scaling and offset will depend on both the individual device and
# application.
calib = linear.map(raw, 59000, 4000, 0.0, 1.0)
# Pipe the calibrated value through all the filters.
filtered = [filt.update(calib) for filt in all_filters]
# Selectively report results for plotting.
# print((raw, calib)) # raw and calibrated input signal
# print((calib, filtered[0][0], filtered[0][1])) # calibrated, average, variance
# print((calib, 1*filtered[1], filtered[2])) # calibrated, thresholded, moving average
print((calib, filtered[3], filtered[4])) # calibrated, smoothed, median-filtered
# print((calib, filtered[5], filtered[6])) # calibrated, low-pass, high-pass
# print((calib, filtered[7], filtered[8])) # calibrated, band-pass, band-stop
Development Tools
The development of these filters involves several other tools:
- A Python script for generating digital filters using SciPy: filter_gen.py
- A Python matplotlib script for generating figures from the test data: generate_plots.py
The Python scripts use several third-party libraries:
- SciPy: comprehensive numerical analysis; linear algebra algorithms used during filter generation
- Matplotlib: plotting library for visualizing data
For more information on filters:
Source: Raspberry pi pico Signal Processing Examples – CircuitPython
